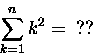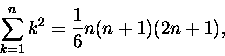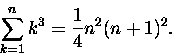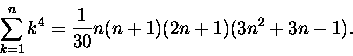Next: Literatura ...
Up: Liczby przeróżne
Previous: Liczby Bernoulliego
Jeżeli funkcję tworzącą liczb Bernoulliego
pomnożyć przez exs to w wyniku dostajemy szereg potęgowy x-a,
którego współczynniki zależą od zmiennej s:
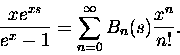 |
(1) |
Może to niezbyt elegancko używać tych samych literek, ale w końcu każdy
widzi, że Bn to liczba, a Bn(s) to funkcja. To, że są bliskimi
krewniaczkami jest ewidentne. Dla s=0 lewe strony obu równań są
identyczne, a więc:
Bn(0) = Bn.
Rozwijając 1 w szereg nietrudno wykazać, że funkcje
Bernoulliego są po prostu wielomianami stopnia n. Jak to bywa w takich
przypadkach (definicja poprzez funkcje tworzące), łatwo można wykazać dwie
podstawowe relacje. Relację rekurencyjną
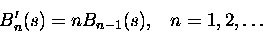 |
(2) |
i relację symetrii
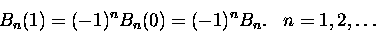 |
(3) |
Te dwie relacje pozwalają wygenerować iteracyjnie wszystkie wielomiany. Na
przykład pierwsze 7 funkcji B. to:
Table 1:
Funkcje Bernoulliego
| B0 |
= |
1 |
| B1 |
= |
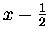 |
| B2 |
= |
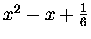 |
| B3 |
= |
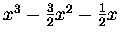 |
| B4 |
= |
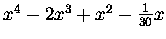 |
| B5 |
= |
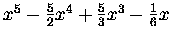 |
| B6 |
= |
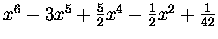 |
Zwróć uwagę na to, że
B0(x) = 1. Zwrócili na to uwagę
(latach trzydziestych XVIII wieku) Leonard Euler, a także - niezależnie -
Maclaurin. Obaj panowie zaproponowali sprytny sposób obliczania sum. Pomysł oparty jest
właśnie na funkcjach B. i na tożsamości:
Nawet komputer widzi, że trzeba całkować przez części:
Ale zgodnie z 2
i zabawę w całkowanie przez części można kontynuować usque ad mortem
maculatam. Wyskakują przy tym wartości funkcji Bernoulliego na krańcach
przedziału - z relacji symetrii 3 wynika, że nieparzyste są równe
zeru,
parzyste - liczbom Bernoulliego:
Nasza całka
![\begin{displaymath}
\int^1_0 f(x) dx = \frac 1 2 [f(1) + f(0)] - \sum_{p=1}^q
\...
...{2p} \left[ f^{(2p-1) }(1)
- f^{(2p-1) }(0) \right] + R_{2q}, \end{displaymath}](emg16.gif) |
(4) |
gdzie różnica R2q to
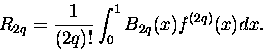 |
(5) |
Wzór 4 trzeba teraz rozszerzyć z przedziału [0,1] na przedział
[1,2] poprzez zamianę f(x) na f(x+1), potem na przedział [2,3] poprzez
zamianę f(x) na f(x+2), potem ....
Zatrzymujemy się na [n-1,n], dodajemy wszystko razem i - kto nie wierzy
niech sobie przerachuje -
gdzie ,,nowa'' różnica RR to
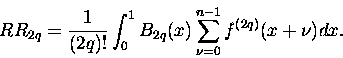 |
(6) |
Czyli rzeczywiście, sumowanie można sobie ,,przybliżać całkowaniem'', a
konkretnie
Druga linijka to nic innego jak całkowanie ,,metodą '' trapezów, natomiast w trzeciej linijce mamy
sumę i całkę 6 . Składniki sumy to liczby Bernoulliego, podzielone przez silnię ich wskaźnika i
pomnożone przez wartości odpowiednich pochodnych na krańcach przedziału całkowania (tylko!
- przy składaniu przyczynków od n przedziałów o jednostkowych szerokościach wyrazy
pośrednie znoszą się!). Natomiast całka 6 wygląda mało sympatycznie, chociaż można
ją nieco upodobnić do ludzi i zapisać w postaci
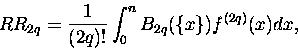 |
(8) |
gdzie 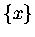 oznacza część ułamkową x-a, to znaczy to
co zostaje z x-a po odjęciu
od niego najbliższej (ale ,,od dołu") liczby całkowitej.
Żeby to jakoś zrozumieć: RR2q
to wartość pochodnej rzędu 2q pomnożona przez ,,coś", co po bliższej analizie okazuje
się niezbyt straszne (zaglądnij do matematyki konkretnej) i przecałkowana po całym
przedziale [0,n] (nierzadko pędzącym do nieskończoności). Zauważ, że całka 8 mimo wszystko
wygląda to już bardziej przyjaźnie, niż 6.
Gdyby tylko nie było RR to sumowanie sprowadzałoby się do:
oznacza część ułamkową x-a, to znaczy to
co zostaje z x-a po odjęciu
od niego najbliższej (ale ,,od dołu") liczby całkowitej.
Żeby to jakoś zrozumieć: RR2q
to wartość pochodnej rzędu 2q pomnożona przez ,,coś", co po bliższej analizie okazuje
się niezbyt straszne (zaglądnij do matematyki konkretnej) i przecałkowana po całym
przedziale [0,n] (nierzadko pędzącym do nieskończoności). Zauważ, że całka 8 mimo wszystko
wygląda to już bardziej przyjaźnie, niż 6.
Gdyby tylko nie było RR to sumowanie sprowadzałoby się do:
- obliczenia całki z f(x)
- obliczenia wartości funkcji i jej kilku (?) kolejnych pochodnych w x=0 i x=n oraz
- przemnożenia tych wartości przez odpowiednie liczby Bernoulliego i dodanie do siebie
A co z tą nieszczęsną resztą RR? Na początek warto zauważyć, że sam Euler specjalnie się nią nie
kłopotał. Wykorzystywał on swój wzór do sumowania f(n), których f(x) miała tę
przyjemną właściwość, że pewna jej pochodna (i następne) stawała się równa
zeru. Na przykład dla f(x) będącą wielomianem stopnia 2m-1 pochodna
stopnia 2m już się zeruje i kładąc w
8 q=m możemy się przestać martwić o
RR. Przybliżony wzór sumacyjny staje się super dokładny. Na przykład sumy Bernoulliego,
takie jak najprostsza
Mamy
f(x) = x2 i zgodnie z receptą 7
Dokładnie! Każdy już potrafi to-to porachować, że
a nieufni zapewne sprawdzą wynik metodą indukcji matematycznej, którą zilustrowaliśmy
właśnie rachowaniem sumy kubek-w-kubek podobnej:
Ambitni zechcą zapewne policzyć powyższą sumę metodą Eulera, a bardzo ambitni
policzą (zupełnie chyba nie do odgadnięcia - aby dało się zastosować indukcję):
Dla mało ambitnych pozostaje zawsze dość trywialne
No, a jeżeli życie nie jest takie różowe?




Next: Literatura ...
Up: Liczby przeróżne
Previous: Liczby Bernoulliego
Andrzej Lenda
1999-05-18
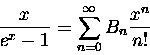
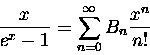
![\begin{eqnarray*}\int^1_0 f(x) dx & = & f(1)B_1(1) - f(0)B_1(0) - \int^1_0 f'(x)...
...x) dx\\
&=& \frac 1 2 [f(1) + f(0)] - \int^1_0 f'(x) B_1(x) dx. \end{eqnarray*}](emg13.gif)

![\begin{eqnarray*}\int^n_0 f(x) dx &=&
\frac 1 2 f(0) + f(1) + f(2) + \ldots + f...
...2p}
\left[ f^{(2p-1) }(n)
- f^{(2p-1) }(0) \right] + RR_{2q}, \end{eqnarray*}](emg18.gif)