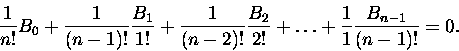Next: ... i pociechy z nich płynące
Up: Magia i mistyka liczb
Previous: Liczby przeróżne
W opublikowanej pośmiertnie Ars Conjectandi Jakuba B. można znaleźć
następujący problem: ile wynosi suma m-tych potęg n kolejnych liczb
całkowitych począwszy od zera? To znaczy, ile wynosi Sm(n):
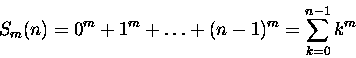 |
(1) |
Chcemy wyrazić wartość sumy przez kombinację liniową potęg liczby n. Dla
m=0 wartość sumy to n jedynek dodanych do siebie, dla m=1 mamy
postęp arytmetyczny, dla m=2 - no tu już trzeba trochę pokombinować,
przy pomocy naszej ulubionej metody - indukcji matematycznej. Jakub
Bernoulli potrafił znaleźć ogólną postać dla kolejnych m. Warto to
zobaczyć:
| S0(n) |
= |
n
|
| S1(n) |
= |
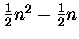
|
| S2(n) |
= |
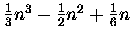
|
| S3(n) |
= |
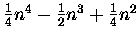
|
| S4(n) |
= |
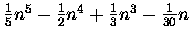
|
| S5(n) |
= |
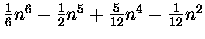
|
| S6(n) |
= |
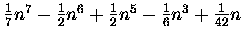
|
| S7(n) |
= |
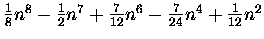
|
| S8(n) |
= |
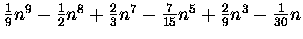
|
| S9(n) |
= |
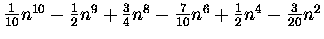
|
| S10(n) |
= |
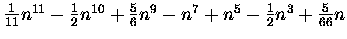 |
Nawet komputer zauważy, że każda suma zaczyna się od potęgi m+1, której współczynnik
to 1/m+1. Współczynnik przy nm to zawsze - 1/2. Współczynnik
przy nm-2 (i kolejnych: m-4, m-6, ...) jest równy zeru. Jeszcze od biedy można zauważyć, że
współczynnik
przy nm-1 jest równy m/12. Dalej zaczynają się
przysłowiowe schody.
Bernoulli nie potrafił znaleźć ogólnych wzorów wiążących
współczynniki poszczególnych potęg w wypisanych powyżej sumach, ale
był przekonany, że te współczynniki muszą być w jakiś sposób ze
sobą powiązane. I rzeczywiście, prace Eulera i innych doprowadziły do
zgrabnego wzoru
Okazuje się więc, że współczynniki zawierają w sobie współczynniki
dwumianowe i pewne liczby Bk, które przyjęło się nazywać
właśnie liczbami Bernoulliego. Prawdę mówiąc, ich obliczanie
nie jest proste. Jeden ze sposobów stanowi wzór rekurencyjny (spokojnie, zaraz go uzasadnimy)
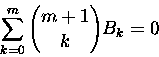 |
(2) |
i przyjęcie B0=1. Dla m=1 powyższa rekurencja daje na przykład
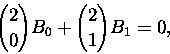 |
(3) |
skąd
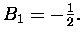 Stosując powyższy wzór można bez większych
kłopotów, ale i bez większej satysfakcji skonstruować tabelkę
Stosując powyższy wzór można bez większych
kłopotów, ale i bez większej satysfakcji skonstruować tabelkę
Brak satysfakcji wynika z dziwacznych postaci uzyskiwanych ułamków -
widać, że trudno liczyć na skwitowanie tematu liczb Bernoulliego
jednym zgrabnym wzorem. Pocieszać(?) nas tylko może zerowanie się
,,nieparzystych'' liczb (za wyjątkiem B1).
Niemniej jednak liczby Bernoulliego pojawiają się często i gęsto, przy
przeróżnych okazjach.
Są absolutnie rewelacyjne do obliczania - dokładnego albo i przyblizonego - sum i właśnie dla tego pociechy z nich płynące
są wielkie.
Najzgrabniej rozmawia się o nich w kontekście teorii
funkcji zmiennej zespolonej. Rozważmy na przykład sympatycznie wyglądająca
funkcję
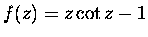 (
(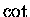 to nie żaden kot, tylko kotangens!). Jest to niewątpliwie funkcja parzysta
(iloczyn
dwóch
funkcji nieparzystych). W zerze nie dzieje się nic złego (pardon, powinienem
powiedzieć: zero jest osobliwością usuwalną) - f(0) = 0 (markiz de l'Hospital
się
kłania), również w nieskończoności f(z) zachowuje się przyzwoicie (pardon,
jest
ograniczona). Ponieważ jednak każda szanująca się funkcja zmiennej zespolonej
musi gdzieś narozrabiać to i f(z) ma swoje momenty szaleństwa. Licznik
kotangensa zeruje się w
to nie żaden kot, tylko kotangens!). Jest to niewątpliwie funkcja parzysta
(iloczyn
dwóch
funkcji nieparzystych). W zerze nie dzieje się nic złego (pardon, powinienem
powiedzieć: zero jest osobliwością usuwalną) - f(0) = 0 (markiz de l'Hospital
się
kłania), również w nieskończoności f(z) zachowuje się przyzwoicie (pardon,
jest
ograniczona). Ponieważ jednak każda szanująca się funkcja zmiennej zespolonej
musi gdzieś narozrabiać to i f(z) ma swoje momenty szaleństwa. Licznik
kotangensa zeruje się w 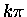 ,
,
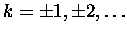 .
Są to zera
pierwszego
rzędu mianownika, a więc bieguny pierwszego rzędu samej f(z). Twierdzenie
Mittag-Lefflera
(praktyczne możliwości tego twierdzenia umiał wykorzystać Euler dobre 100 lat
wcześniej) mówi, że taka funkcja meromorficzna
może zostać rozłożona skutecznie na ułamki proste, według ogólnego wzoru
.
Są to zera
pierwszego
rzędu mianownika, a więc bieguny pierwszego rzędu samej f(z). Twierdzenie
Mittag-Lefflera
(praktyczne możliwości tego twierdzenia umiał wykorzystać Euler dobre 100 lat
wcześniej) mówi, że taka funkcja meromorficzna
może zostać rozłożona skutecznie na ułamki proste, według ogólnego wzoru
![\begin{displaymath}f(z) = \sum_{k} \left( \frac{1}{z - z_k} + \frac{1}{ z_k} \right) \times
[{reziduum} \,f(z); z=z_k],
\end{displaymath}](bmg21.gif) |
(4) |
gdzie zk są biegunami naszej funkcji; sumujemy po wszystkich - dodatnich i ujemnych - biegunach.
W przypadku naszego sympatycznego kotangensa jego wszystkie
rezidua w biegunach
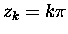 ,
są równe jedności i wzór się znakomicie
upraszcza
,
są równe jedności i wzór się znakomicie
upraszcza
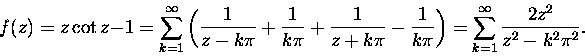 |
(5) |
Funkcja jest parzysta, więc wypadałoby aby suma dała się
przedstawić w
postaci szeregu potęgowego o wyłącznie parzystych potęgach. A ponieważ mówi się
tutaj o liczbach Bernoulliego ..., no właśnie zgadłeś:
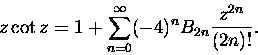 |
(6) |
Mamy parzyste potęgi z-a, a ich współczynniki to liczby Bernoulliego,
podzielone
przez silnię wskaźnika (zauważ jak to ładnie musi wpływać na zbieżność szeregu).
O
takich detalach jak (-4)n nie warto wspominać.
Wzór Eulera (5) można jednak spróbować naprawdę rozwinąć
względem potęg z2. Wystarczy licznik i mianownik wyrażenia pod znakiem sumy
podzielić przez z2 (znak się przy okazji "niechcący" zmienił; przepraszam - nie będę juz przerabiał gif-a!):
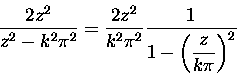 |
(7) |
i potraktować drugi czynnik jako sumę postępu geometrycznego (kwestia czy
wolno tak postępować - wolno, ale spróbuj to sobie wytłumaczyć.) No a jeśli
tak, to
W naszym poczciwym i sympatycznym, przemnożonym przez z, kotangensie odkrywamy nagle oszałamiające
skarby: współczynniki rozwinięcia tego iloczynu w szereg parzystych potęg z-a to
nieskończone sumy - szeregi -
odwrotności parzystych potęg liczb naturalnych. Co więcej, wszystkie te
szeregi
mamy już posumowane - ich wartości to liczby Bernoulliego, potraktowane
odpowiednimi potęgami 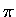 i silniami!
Warto tutaj podać pewne definicje i związki. Suma m składników
i silniami!
Warto tutaj podać pewne definicje i związki. Suma m składników
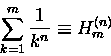 |
(9) |
nazywa się uogólniooną liczbą harmoniczną rzędu n. (Dla n=1
mamy ,,zwykłe'' liczby harmoniczne.) Jeżeli
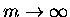 to taka
nieskończona suma nazywa się funkcją dzeta Riemanna:
to taka
nieskończona suma nazywa się funkcją dzeta Riemanna:
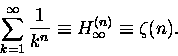 |
(10) |
Z powyższych zabaw wynika więc, że (wzory: 5, 8 i 10):
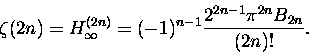 |
(11) |
To naprawdę nie byle co. Jeżeli policzyć (według rekurencji 2) parę
liczb
Bernoulliego to świat sum typu
nie ma dla nas tajemnic! Na przykład:
Zapewne znasz kilka innych sposobów policzenia powyższych sum, ale przyznaj,
że
ten z liczbami Bernoulliego to elegancja + skuteczność w najlepszym wydaniu!
Ludzie, którzy lubią porządek i systematyczność woleliby zapewne zamiast ,,poczciwego kotangensa''
(5) mieć do czynienia z funkcją, której rozwinięcie w szereg potęgowy zawierałoby wszystkie
liczby Bernoulliego. (W rozwinięciu
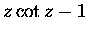 brakuje jedynej różnej od zera
nieparzystej B!). Słusznie. Jest taka funkcja i też całkiem przyjazna:
brakuje jedynej różnej od zera
nieparzystej B!). Słusznie. Jest taka funkcja i też całkiem przyjazna:
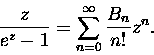 |
(14) |
Z powyższego wzoru wynika kolejny pomysł na obliczanie Bn:
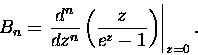 |
(15) |
Liczenie pochodnych to jednak zajęcie, które choć metodycznie łatwe, bywa mocno uciążliwe.
Jeżeli skorzystać z wzoru całkowego Cauchy na n-ty współczynnik w rozwinięciu Taylora (14)
to z teorii funkcji zmiennej zespolonej wynika, że:
gdzie jako kontur C0 dla n=0,1 warto wybrać koło 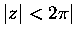 (dlaczego?).
Aby obliczyć Bn dla
(dlaczego?).
Aby obliczyć Bn dla 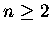 wygodniej jest zmodyfikować
,
wygodniej jest zmodyfikować
, ,
(dlaczego?):
,
(dlaczego?):
Nowy kontur obejmuje wszystkie bieguny pierwszego rzędu:
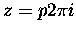 ,
w których residua funkcji podcałkowej wynoszą:
,
w których residua funkcji podcałkowej wynoszą:
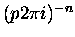 .
A więc (dla n parzystego dodatnie przyczynki podwajają się; dla n <0 - redukują się do
zera):
.
A więc (dla n parzystego dodatnie przyczynki podwajają się; dla n <0 - redukują się do
zera):
dla 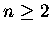 i parzystego. Dla
i parzystego. Dla
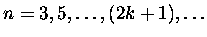 Bn = 0.
Bn = 0.
Jak widać kółko się zamknęło. Po raz drugi skojarzyliśmy Bn z odpowiednią dzetą Riemanna.
Na zakończenie: skąd bierze się rekurencja 2? Przypatrzmy się funkcji tworzącej 14. Mamy:
Innymi słowy
Teraz już tylko pozostało pomnożyć dwie nieskończone sumy po lewej stronie i tak pogrupować wyrazy, aby
lewa strona miała postać sumy
Prawa strona to też taka suma, z c0 = 1 i
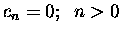 .
A więc b0 = 1, a współczynnik przy cn
(n>0), to
.
A więc b0 = 1, a współczynnik przy cn
(n>0), to
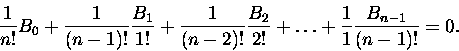 |
(16) |
Pomnożenie powyższego równania przez n! i zidentyfikowanie odpowiednich iloczynów (ilorazów) silni jako
współczynników dwumianowych prowadzi do rekurencji 2.




Andrzej Lenda
1999-04-19
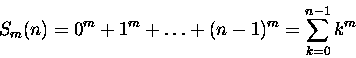
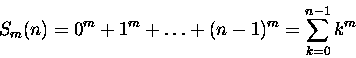
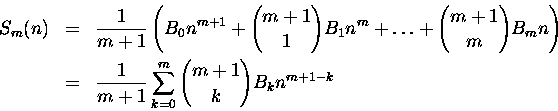
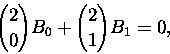
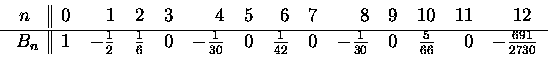
![]() (
(![]() to nie żaden kot, tylko kotangens!). Jest to niewątpliwie funkcja parzysta
(iloczyn
dwóch
funkcji nieparzystych). W zerze nie dzieje się nic złego (pardon, powinienem
powiedzieć: zero jest osobliwością usuwalną) - f(0) = 0 (markiz de l'Hospital
się
kłania), również w nieskończoności f(z) zachowuje się przyzwoicie (pardon,
jest
ograniczona). Ponieważ jednak każda szanująca się funkcja zmiennej zespolonej
musi gdzieś narozrabiać to i f(z) ma swoje momenty szaleństwa. Licznik
kotangensa zeruje się w
to nie żaden kot, tylko kotangens!). Jest to niewątpliwie funkcja parzysta
(iloczyn
dwóch
funkcji nieparzystych). W zerze nie dzieje się nic złego (pardon, powinienem
powiedzieć: zero jest osobliwością usuwalną) - f(0) = 0 (markiz de l'Hospital
się
kłania), również w nieskończoności f(z) zachowuje się przyzwoicie (pardon,
jest
ograniczona). Ponieważ jednak każda szanująca się funkcja zmiennej zespolonej
musi gdzieś narozrabiać to i f(z) ma swoje momenty szaleństwa. Licznik
kotangensa zeruje się w ![]() ,
,
![]() .
Są to zera
pierwszego
rzędu mianownika, a więc bieguny pierwszego rzędu samej f(z). Twierdzenie
Mittag-Lefflera
(praktyczne możliwości tego twierdzenia umiał wykorzystać Euler dobre 100 lat
wcześniej) mówi, że taka funkcja meromorficzna
może zostać rozłożona skutecznie na ułamki proste, według ogólnego wzoru
.
Są to zera
pierwszego
rzędu mianownika, a więc bieguny pierwszego rzędu samej f(z). Twierdzenie
Mittag-Lefflera
(praktyczne możliwości tego twierdzenia umiał wykorzystać Euler dobre 100 lat
wcześniej) mówi, że taka funkcja meromorficzna
może zostać rozłożona skutecznie na ułamki proste, według ogólnego wzoru
![\begin{displaymath}f(z) = \sum_{k} \left( \frac{1}{z - z_k} + \frac{1}{ z_k} \right) \times
[{reziduum} \,f(z); z=z_k],
\end{displaymath}](bmg21.gif)
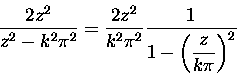
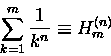
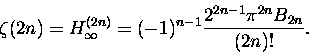
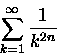
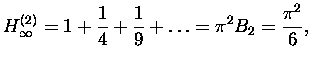
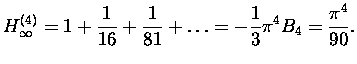
![]() brakuje jedynej różnej od zera
nieparzystej B!). Słusznie. Jest taka funkcja i też całkiem przyjazna:
brakuje jedynej różnej od zera
nieparzystej B!). Słusznie. Jest taka funkcja i też całkiem przyjazna:
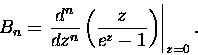
 ,
(dlaczego?):
,
(dlaczego?):
![]() ,
w których residua funkcji podcałkowej wynoszą:
,
w których residua funkcji podcałkowej wynoszą:
![]() .
A więc (dla n parzystego dodatnie przyczynki podwajają się; dla n <0 - redukują się do
zera):
.
A więc (dla n parzystego dodatnie przyczynki podwajają się; dla n <0 - redukują się do
zera):
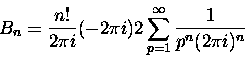
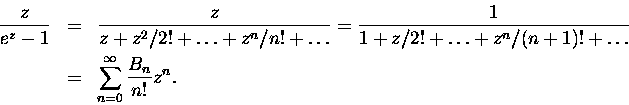
![\begin{eqnarray*}\left[ 1+ z/2! + z^2/3! + \ldots + z^{n}/(n+1)! + \ldots + \rig...
..._2}{2!} z^2 + \ldots + \frac{B_n}{n!} z^n + \ldots \right] = 1 . \end{eqnarray*}](bmg50.gif)