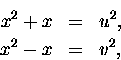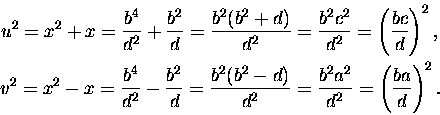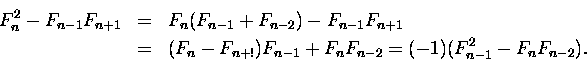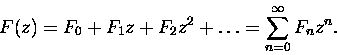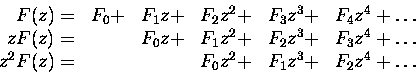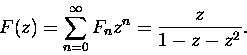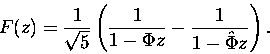Next: Literatura ...
Up: Liczby Bernoulliego
Previous: Liczby przeróżne
 Bez większej przesady można powiedzieć, że europejska
matematyka po wielu wiekach
uśpienia zaczęła się odradzać na przełomie XII i XIII wieku i to za sprawą jednego
człowieka.
Był nim Pizańczyk - Leonardo Fibonacci (circa 1170 - circa 1240). To sympatycznie
brzmiące nazwisko kryje w sobie łacińskie filius Bonacci, czyli syn Bonacciego; z
kolei Bonaccio możnaby (z grubsza) tłumaczyć jako: poczciwiec. Wspominamy o
ojcu, bo prawdopodobnie jemu zawdzięczamy porednio sukcesy syna. Bonaccio, pizański
kupiec, był szefem włoskiej kolonii w północno-afrykańskim porcie Boużia (dziś algierska
Beżaja). Tam Leonardo pobierał pierwsze lekcje matematyki u arabskiego nauczyciela.
Widocznie dobrze się sprawował bo dalsze studia zawiodły go w rozliczne miejsca. Były to
Egipt, Syria, Prowansja, Grecja i Sycylia - nieźle jak na 12-wiecznego studenta. Po powrocie
do Pizy, w 1202 roku, Leonardo napisał swoje głośne dzieło Liber Abaci
(Księga Rachunków), w której pojawiają się, i to w pierwszym rozdziale, arabskie a raczej
hinduskie cyfry. Warto tu wspomnieć, że ten dla nas tak dzisiaj naturalny system, wędrował do
Europy za pośrednictwem Arabów dobre parę setek lat.
To warto zobaczyć - jak hinduskie znaczki, za pośrednictwem przedsiębiorczych Arabów, docierały do Europy. Nota bene: słynny wynalazek hinduski - zero,
pojawiło się około IV-V wieku po Chrystusie, początkowo w formie kropki. Wraz z jego pojawieniem rozpoczął się dziesiętny system pozycyjny.
Bez większej przesady można powiedzieć, że europejska
matematyka po wielu wiekach
uśpienia zaczęła się odradzać na przełomie XII i XIII wieku i to za sprawą jednego
człowieka.
Był nim Pizańczyk - Leonardo Fibonacci (circa 1170 - circa 1240). To sympatycznie
brzmiące nazwisko kryje w sobie łacińskie filius Bonacci, czyli syn Bonacciego; z
kolei Bonaccio możnaby (z grubsza) tłumaczyć jako: poczciwiec. Wspominamy o
ojcu, bo prawdopodobnie jemu zawdzięczamy porednio sukcesy syna. Bonaccio, pizański
kupiec, był szefem włoskiej kolonii w północno-afrykańskim porcie Boużia (dziś algierska
Beżaja). Tam Leonardo pobierał pierwsze lekcje matematyki u arabskiego nauczyciela.
Widocznie dobrze się sprawował bo dalsze studia zawiodły go w rozliczne miejsca. Były to
Egipt, Syria, Prowansja, Grecja i Sycylia - nieźle jak na 12-wiecznego studenta. Po powrocie
do Pizy, w 1202 roku, Leonardo napisał swoje głośne dzieło Liber Abaci
(Księga Rachunków), w której pojawiają się, i to w pierwszym rozdziale, arabskie a raczej
hinduskie cyfry. Warto tu wspomnieć, że ten dla nas tak dzisiaj naturalny system, wędrował do
Europy za pośrednictwem Arabów dobre parę setek lat.
To warto zobaczyć - jak hinduskie znaczki, za pośrednictwem przedsiębiorczych Arabów, docierały do Europy. Nota bene: słynny wynalazek hinduski - zero,
pojawiło się około IV-V wieku po Chrystusie, początkowo w formie kropki. Wraz z jego pojawieniem rozpoczął się dziesiętny system pozycyjny.
Pierwszy i drugi wiersz - to hinduskie cyfry z drugiego i ósmego wieku;
trzeci i czwarty - arabska Hiszpania - dziesiąty wiek.
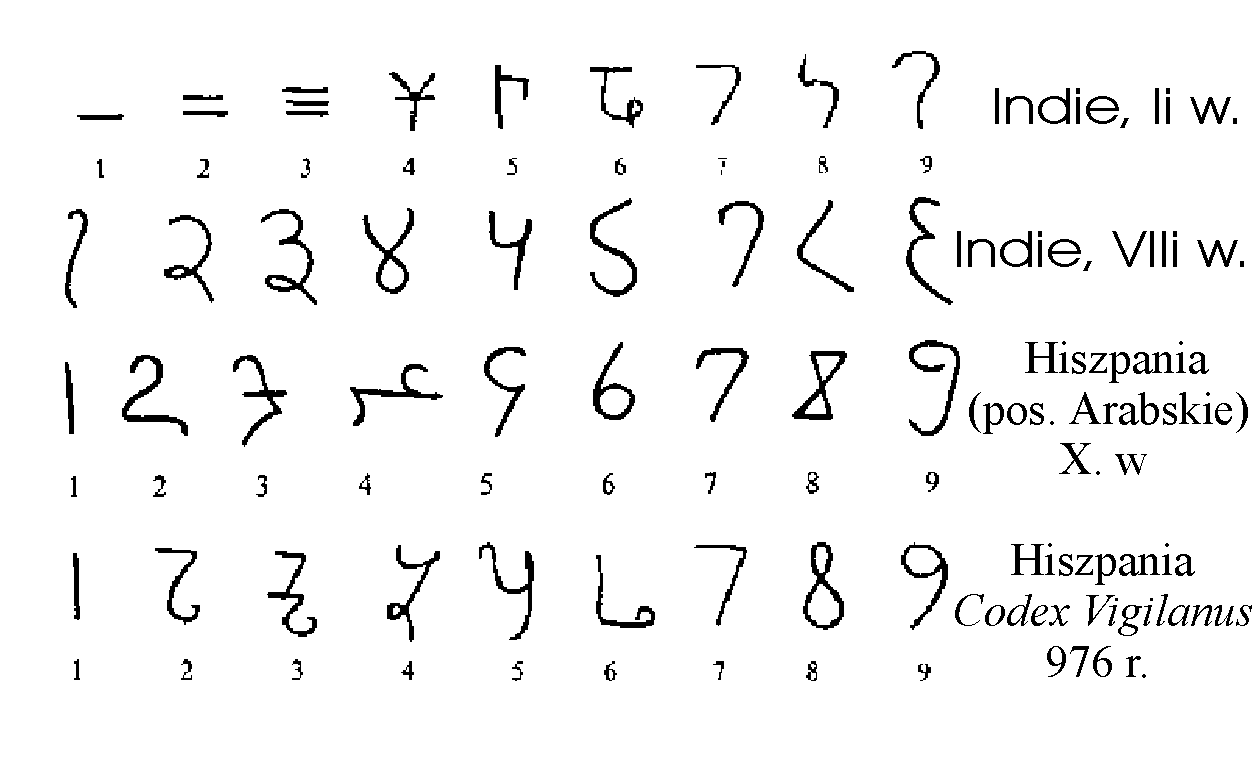 Ze względu na skomplikowane (?) i różne (!) formy zapisu
nowy sposób kodowania
przyjmował się opornie jeszcze w 1229 roku rada miejska
Florencji zabroniła używania arabskich cyfr, nakazując posługiwanie się
symbolami rzymskimi lub wypisywanie liczb ,,słownie''. Powodem były ...częste fałszerstwa.
Zero
można było łatwiutko przerobić na 6 lub 9, a w ogóle taka cyfra która przedstawia sobą
,,nic''
długo nie docierała do świadomości średniowiecznych rachmistrzów. Zasługa No. 1
Fibonacciego to definitywne spopularyzowanie arabskiego systemu numerycznego.
Ze względu na skomplikowane (?) i różne (!) formy zapisu
nowy sposób kodowania
przyjmował się opornie jeszcze w 1229 roku rada miejska
Florencji zabroniła używania arabskich cyfr, nakazując posługiwanie się
symbolami rzymskimi lub wypisywanie liczb ,,słownie''. Powodem były ...częste fałszerstwa.
Zero
można było łatwiutko przerobić na 6 lub 9, a w ogóle taka cyfra która przedstawia sobą
,,nic''
długo nie docierała do świadomości średniowiecznych rachmistrzów. Zasługa No. 1
Fibonacciego to definitywne spopularyzowanie arabskiego systemu numerycznego.
W Liber Abaci można znaleźć szereg ciekawych problemów matematycznych. Może masz
ochotę rozwiązać problem o dwóch ptakach, albo o kupcu z Pizy, czy też o zawartościach
czterech sakiewek? Za łatwe? To może zagadkę Jana z Palermo, nadwornego matematyka Fryderyka II na
jego sycylijskim dworze?
Były też tam ulubione przez matematyków arabskich równania diofantyńskie
(Diofantes, grecki matematyk z Aleksandrii, III w.). Takie równanie diofantyńskie to równanie z
dwoma
niewiadomymi, np.
6x - 9y = 29,
którego (zazwyczaj nieskończenie wiele) rozwiązań
poszukujemy
w klasie liczb całkowitych, albo przynajmniej wymiernych. Łatwo spostrzec, że w takiej sytuacji
rozwiązań nie ma: 6x i 9y to liczby całkowite podzielne przez 3, a 29 przez
trzy się nie
dzieli.
Wystarczy jednak lekko go zmienić
6x - 9y = 30
i rozwiązań w postaci
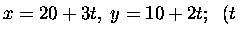 całkowite) mamy nieskończenie wiele.
całkowite) mamy nieskończenie wiele.
Tour de force Fibonacciego to rozwiązanie równania trzeciego stopnia
x3 + 2x2 + 10x = 20.
Był to jeden z piętnastu problemów, które przedstawiono do rozwiązania Leonardowi na dworze
cesarza Fryderyka II (dobra książka: Steven Runciman, Nieszpory Sycylijskie, Książnica 1997).
Leonardo poradził sobie z tym równaniem metodą prób i błędów. Jego rozwiązanie
podane w
notacji
sześćdziesiątkowej
to w notacji dziesiętnej 1,3688081075. Naprawdę warto sprawdzić, że jest to przybliżone
rozwiązanie
jest poprawne do przedostatniego (!) miejsca po przecinku włącznie.
W 1225 Fibonacci opublikował kolejne dzieło Liber quadratorum, poświęcone
wyłącznie
równaniom diofantyńskim, ale z niewiadomymi w drugiej potędze. Takim typowym problemem
jest na
przykład układ:
w którym x, u i v są niewiadomymi.
Rozwiązania tego układu - w klasie liczb wymiernych -
poszukiwał F. rozważając ciąg trzech liczb
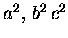 - kwadratów liczb całkowitych -
które
tworzą postęp arytmetyczny o różnicy d:
- kwadratów liczb całkowitych -
które
tworzą postęp arytmetyczny o różnicy d:
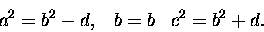 |
(1) |
Wystarczy teraz wpaść na to, aby niewiadomą x przedstawić w postaci ułamka (liczba
wymierna!)
b2/d; pozostałe kwadraty niewiadomych to
Proste. Wystarczy tylko na to wpaść. Najprostsze rozwiązanie diofantyny 1 - jedno z
nieskończenie wielu -
można uzyskać kładąc a = 1 (jak najprostsze, to najprostsze) i poszukując
takich b i c, żeby 2b2 - 1 było kwadratem
całkowitej liczby. Spróbuj. Nie trzeba daleko
szukać.
A jeżeli masz ochotę zmierzyć się z mistrzem to kolejny problem z Liber quadratorum:
Udowodnij, że jeżeli suma dwóch kolejnych liczb całkowitych jest kwadratem pewnej liczby, to większy składnik tej sumy daje się zapisać jako suma
dwóch kwadratów (liczb całkowitych).
Leonardo Fibonacci sumiennie przestudiował i przyswoił sobie ówczesną wiedzę
matematyczną.
Co więcej - potrafił sam w sposób znaczący tę wiedzę wzbogacić. Jego prace
dotyczące teorii
liczb
(np. zagadnienie kongruencji) musiały czekać 400 lat na kontynuatorów. To jednak, że nazwisko
Fibonacciego weszło do matematyki to zasługa pewnego ciągu liczb, nazwanego (dopiero w XIX
w. przez francuskiego matematyka, Edwarda Lucasa) ciągiem Fibonacciego. Jak zwykle - to nie
Leonardo ,,wymyślił'' ten ciąg. Ale w jego Liber Abaci jest taki oto problem:
Pewien gospodarz zamknął w dużej klatce parę królików.
Ile par królików będzie w klatce po
roku, jeżeli każda para królików co miesiąc rodzi nową
parę, a ta staje się ,,reproduktywna'' po
upływie miesiąca?
|
Miesiąc |
Pary |
Pary |
Całkowita |
| |
dorosłe |
młode |
liczba par |
| 1 |
1 |
1 |
2 |
| 2 |
2 |
1 |
3 |
| 3 |
3 |
2 |
5 |
| 4 |
5 |
3 |
8 |
| 5 |
8 |
5 |
13 |
| 6 |
13 |
8 |
21 |
| 7 |
21 |
13 |
34 |
| 8 |
34 |
21 |
55 |
| 9 |
55 |
34 |
89 |
| 10 |
89 |
55 |
144 |
| 11 |
144 |
89 |
233 |
| 12 |
233 |
144 |
377 |
Nietrudno zauważyć, że liczba par w kolejnym miesiącu
to suma dwóch składników: liczby par
poprzedniego miesiąca, powiększonej o liczbę par przychówku.
Ta ostatnia liczba jest równa
liczbie par sprzed dwóch miesięcy. Liczby Fibonacciego to
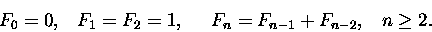 |
(2) |
(Dodanie dwóch jedynek na początku można też interpretować przy pomocy
królików:
jeżeli para
została zamknięta w klatce zaraz po urodzeniu to po miesiącu w klatce ciągle była tylko ta jedna
parka. Zero - no cóż, od czegoś trzeba zacząć)
Liczby Fibonacciego są przykładem ciągu rekurencyjnego liczb całkowitych,
który posiada cały
szereg zaskakujących własności. Na przykład:
- Dwie kolejne liczby F. nie mają wspólnego podzielnika
(z wyjątkiem trywialnego 1).
Dowód metodą nie wprost:
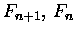 są
podzielne przez pewną liczbę d. Z rekurencji
2 wynika,
że Fn-1 będzie też podzielne przez d. Ale
w takim razie Fn-2 też
(stosujemy rekurencje do trójki o
indeksach n,n-1,n-2), podobnie jak
są
podzielne przez pewną liczbę d. Z rekurencji
2 wynika,
że Fn-1 będzie też podzielne przez d. Ale
w takim razie Fn-2 też
(stosujemy rekurencje do trójki o
indeksach n,n-1,n-2), podobnie jak
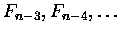 .
Cofając się n kroków wstecz dostajemy, że F1 = 1 też jest podzielne przez
d.
.
Cofając się n kroków wstecz dostajemy, że F1 = 1 też jest podzielne przez
d.
- Dla dowolnej liczby pierwszej p mamy nieskończenie wiele liczb F, które są podzielne
przez p, i które są rozmieszczone w równych odstępach w ciągu. Każdy ,,co czwarty'' wyraz
ciągu jest na przykład podzielny przez 3, co piąty - przez 5, co ósmy przez 7, itd.
- Liczby spełniają relację
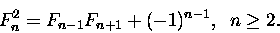 |
(3) |
Dowód znowu jest oparty na 2
Obniżyliśmy wartości wszystkich wskaźników o jedynkę. Postępując tak n-
2 razy
dostaniemy Fn2 - Fn-
1Fn+1 = (-1)n-2
(F22 - F3F1)= (-
1)n-1.
Ta sympatyczna relacja, opublikowana po raz pierwszy w 1650r. (Kepler znał ją 50 lat wcześniej!)
przez Jean Dominique Cassiniego (tego od
przerwy Cassiniego w pierścieniach Saturna), przy
podstawieniu n=2k staje się podstawą paradoksu Cassiniego, ulubionej ponoć
łamigłówki
Lewisa Carolla (autor ,,Alicji w krainie czarów'' był nauczycielem matematyki!). Mamy
F22k = F2k-
1F2k+1 - 1.
Hmm, to teraz podziel sobie robaczku szachownicę na cztery części i ułóż z niej prostokąt.
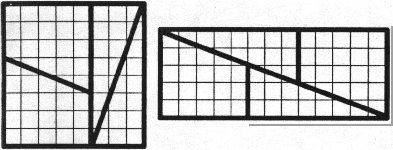 .
Miałeś
.
Miałeś
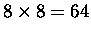 kwadraciki , masz
kwadraciki , masz
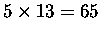 .
Wystarczy by bok
kwadratu był liczbą Fibonacciego, aby posklejany z niego kawałków prostokąt miał pole o
jednostkę
większą lub mniejszą. Nie słyszałeś pewno nigdy o prawie zachowania powierzchni, ale tak na
zdrowy rozum to powinno takie prawo istnieć. Czyżby liczby F nie musiały mu się
podporządkowywać?
.
Wystarczy by bok
kwadratu był liczbą Fibonacciego, aby posklejany z niego kawałków prostokąt miał pole o
jednostkę
większą lub mniejszą. Nie słyszałeś pewno nigdy o prawie zachowania powierzchni, ale tak na
zdrowy rozum to powinno takie prawo istnieć. Czyżby liczby F nie musiały mu się
podporządkowywać?
Pomyślałeś już - choć trochę - o tym dziwnym zjawisku. No to , z tych samych kawałków szachownicy ułóż
cos bardziej skomplikowanego:
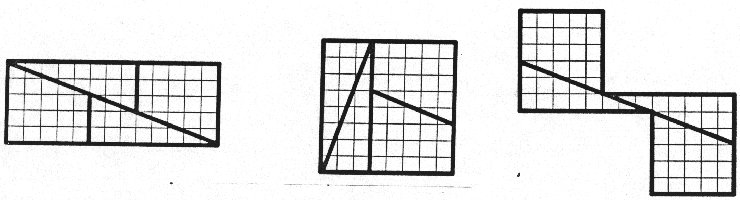 .
Miałeś 64 kwadraciki, masz 63. No więc?
.
Miałeś 64 kwadraciki, masz 63. No więc?
- Liczby Fibonacciego tworzą system liczbowy. To znaczy każda liczba całkowita może
być przedstawiona jako suma liczb Fibonaciego. Każda! Jeden milion w reprezentacji Fibonacciego
wygląda o tak:
| 1 000 000 |
= |
83 2040 + |
121 393 + |
46 368 + |
144 + |
55 |
| |
= |
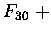 |
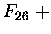 |
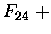 |
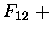 |
F10 |
| |
= |
(100010100000000000101000000000)F |
Te zera i jedynki to - oczywicie - brak (0) albo obecność (1) liczby o danym wskaźniku;
zaczynamy od prawej strony - najbardziej skrajne zero odpowiada F1.
- Liczby Fibonacciego mają swoją funkcję tworzącą, tzn. istnieje szereg potęgowy
Fz:
Rekurencja 2 pozwala nam ten szereg
znaleźć natychmiast. Mnożąc powyższy szereg przez z i z2
mamy
Po odjęciu dwóch ostatnich równań od pierwszego wyrazy z potęgami z2,
z3, ...znikną - bo
ich ,,wypadkowe'' współczynniki są równe zeru (rekurencja Fibonacciego!). Wszystko co zostanie
po odjęciu to
F0 + (F1 - F0)z =
z(F0 = 0). No i proszę
|
F(z) - zF(z) - z2F(z) = z
,
|
(4) |
albo
Ten zgrabny wzór staje się jeszcze zgrabniejszy jeżeli rozbić go
na ułamki proste.
(Jeżeli sam nie potrafisz to zaglądnij do Literatury - a konkretnie, do ...
no właśnie, Matematyki konkretnej). Po niezbyt trudnych zabiegach okazuje się, że
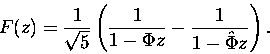 |
(5) |
Tajemnicze 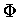 i
i 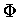 z daszkiem to baaardzo ważne stałe. Liczba
z daszkiem to baaardzo ważne stałe. Liczba
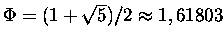 to słynny złoty stosunek, znany jeszcze starożytnym artystom. (Dlatego ,,Fi'' jak Fidiasz). Fi z
daszkiem to
to słynny złoty stosunek, znany jeszcze starożytnym artystom. (Dlatego ,,Fi'' jak Fidiasz). Fi z
daszkiem to
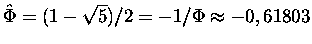 .
.
Także Fibonacciemu przypisuje sie konstrukcję ładnie ilustrującą
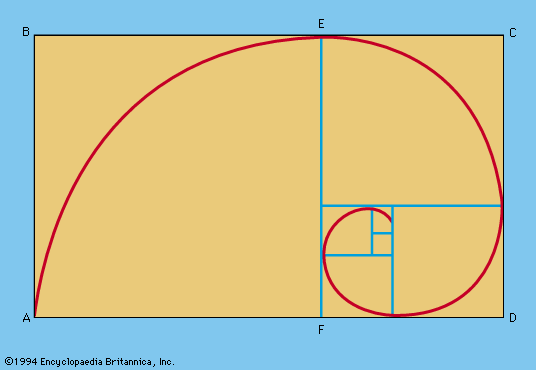 .
Prostokąt ABCD jest zbudowany ze "złotych odcinków". Wycinając z niego kwadrat ABEF zbudowany na krótszym boku dostajemy kolejny
złoty prostokąt ECDF
(bokiem krótszym "do góry"). I tak dalej. łącząc wierzchołki kolejnych kwadratów dostajemy spiralę Fibonacciego. Dlaczego Fibonacciego?
Spróbuj pomyśleć, że dwa najmniejsze czworokąty to - praktycznie - takie same, ,,jednostkowe" kwadraty. Ten następny to kwadrat o boku 2,
kolejny kwadrat ma bok równy 3, kolejny - 5...
A więc?
.
Prostokąt ABCD jest zbudowany ze "złotych odcinków". Wycinając z niego kwadrat ABEF zbudowany na krótszym boku dostajemy kolejny
złoty prostokąt ECDF
(bokiem krótszym "do góry"). I tak dalej. łącząc wierzchołki kolejnych kwadratów dostajemy spiralę Fibonacciego. Dlaczego Fibonacciego?
Spróbuj pomyśleć, że dwa najmniejsze czworokąty to - praktycznie - takie same, ,,jednostkowe" kwadraty. Ten następny to kwadrat o boku 2,
kolejny kwadrat ma bok równy 3, kolejny - 5...
A więc?
Postać funkcji tworzącej 5 i jej definicja pozwala nam określić liczby F
jako
Dla dużych n przyczynek od
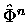 staje się zaniedbywalnie mały i Fn staje się
praktycznie równe n-tej potędze złotego stosunku podzielonej przez
staje się zaniedbywalnie mały i Fn staje się
praktycznie równe n-tej potędze złotego stosunku podzielonej przez 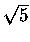 .
A jeżeli tak to
iloraz dwóch kolejnych liczb F staje się z coraz lepszym przybliżeniem równy
.
A jeżeli tak to
iloraz dwóch kolejnych liczb F staje się z coraz lepszym przybliżeniem równy 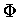 !
!
Podane powyżej własności liczb Fibonacciego to tylko te najważniejsze. Ale nie tylko ich
fascynujące własności są godne zainteresowania. Liczby F manifestują się w otaczającym
nas wiecie w przedziwny sposób. Wiadomo, że truteń (samiec pszczoły) rodzi się
bezpłciowo z samicy (królowej, czyli ma jedną mamę i nie ma ojca. Ale jego mama - królowa,
jak każda samica musi mieć dwoje rodziców. A więc truteń ma jednego dziadka i jedną
babcię, jednego pradziadka ale już dwie prababcie, dwóch prapradziadków i trzy praprababcie.
Sprawdź: truteń ma Fn+1 pran-
dziadków i Fn+2 pran-babć.
Promień świetlny przechodząc przez dwie położone na siebie szyby może się odbić n
razy od trzech powierzchni granicznych (powietrze-szkło; szkło-szkło; szkło-powietrze). Parzyste
n (łącznie z zerem) odpowiada przejściu przez szyby; dla n nieparzystego
promień ,,zawraca''.
Jeżeli policzyć liczby różnych przejść przy n-krotnym odbiciu to ...
 .
.
Zupełnie zadziwiające jest to, że liczby F spotykamy w przyrodzie. No może nie zupełnie zadziwiające - widzieliśmy jak to sprawy mają się z przodkami trutnia.
Poczciwy słonecznik ma
głowę składającą się ze spirali upakowanych
nasion: 34 zwoje w jednym kierunku i 55 w drugim. Małe głowy maja odpowiednio 21 i 34 zwoi, albo 13 i
21. Szyszki drzew iglastych, owoce ananasa - potrafią mieć podobne struktury!




Next: LiteraturaA>
Up: Liczby Bernoulliego
Previous: Liczby przeróżne
Andrzej Lenda
1999-04-26
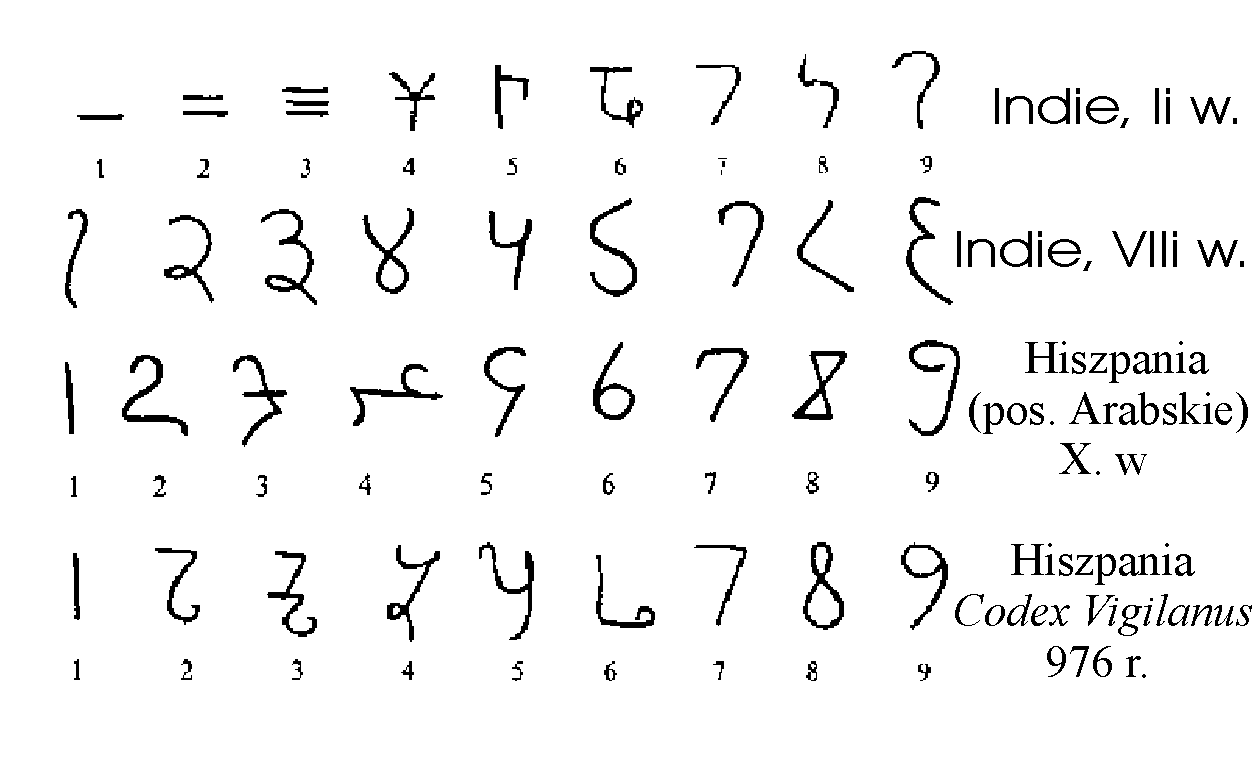 Ze względu na skomplikowane (?) i różne (!) formy zapisu
nowy sposób kodowania
przyjmował się opornie jeszcze w 1229 roku rada miejska
Florencji zabroniła używania arabskich cyfr, nakazując posługiwanie się
symbolami rzymskimi lub wypisywanie liczb ,,słownie''. Powodem były ...częste fałszerstwa.
Zero
można było łatwiutko przerobić na 6 lub 9, a w ogóle taka cyfra która przedstawia sobą
,,nic''
długo nie docierała do świadomości średniowiecznych rachmistrzów. Zasługa No. 1
Fibonacciego to definitywne spopularyzowanie arabskiego systemu numerycznego.
Ze względu na skomplikowane (?) i różne (!) formy zapisu
nowy sposób kodowania
przyjmował się opornie jeszcze w 1229 roku rada miejska
Florencji zabroniła używania arabskich cyfr, nakazując posługiwanie się
symbolami rzymskimi lub wypisywanie liczb ,,słownie''. Powodem były ...częste fałszerstwa.
Zero
można było łatwiutko przerobić na 6 lub 9, a w ogóle taka cyfra która przedstawia sobą
,,nic''
długo nie docierała do świadomości średniowiecznych rachmistrzów. Zasługa No. 1
Fibonacciego to definitywne spopularyzowanie arabskiego systemu numerycznego.
 Bez większej przesady można powiedzieć, że europejska
matematyka po wielu wiekach
uśpienia zaczęła się odradzać na przełomie XII i XIII wieku i to za sprawą jednego
człowieka.
Był nim Pizańczyk - Leonardo Fibonacci (circa 1170 - circa 1240). To sympatycznie
brzmiące nazwisko kryje w sobie łacińskie filius Bonacci, czyli syn Bonacciego; z
kolei Bonaccio możnaby (z grubsza) tłumaczyć jako: poczciwiec. Wspominamy o
ojcu, bo prawdopodobnie jemu zawdzięczamy porednio sukcesy syna. Bonaccio, pizański
kupiec, był szefem włoskiej kolonii w północno-afrykańskim porcie Boużia (dziś algierska
Beżaja). Tam Leonardo pobierał pierwsze lekcje matematyki u arabskiego nauczyciela.
Widocznie dobrze się sprawował bo dalsze studia zawiodły go w rozliczne miejsca. Były to
Egipt, Syria, Prowansja, Grecja i Sycylia - nieźle jak na 12-wiecznego studenta. Po powrocie
do Pizy, w 1202 roku, Leonardo napisał swoje głośne dzieło Liber Abaci
(Księga Rachunków), w której pojawiają się, i to w pierwszym rozdziale, arabskie a raczej
hinduskie cyfry. Warto tu wspomnieć, że ten dla nas tak dzisiaj naturalny system, wędrował do
Europy za pośrednictwem Arabów dobre parę setek lat.
To warto zobaczyć - jak hinduskie znaczki, za pośrednictwem przedsiębiorczych Arabów, docierały do Europy. Nota bene: słynny wynalazek hinduski - zero,
pojawiło się około IV-V wieku po Chrystusie, początkowo w formie kropki. Wraz z jego pojawieniem rozpoczął się dziesiętny system pozycyjny.
Bez większej przesady można powiedzieć, że europejska
matematyka po wielu wiekach
uśpienia zaczęła się odradzać na przełomie XII i XIII wieku i to za sprawą jednego
człowieka.
Był nim Pizańczyk - Leonardo Fibonacci (circa 1170 - circa 1240). To sympatycznie
brzmiące nazwisko kryje w sobie łacińskie filius Bonacci, czyli syn Bonacciego; z
kolei Bonaccio możnaby (z grubsza) tłumaczyć jako: poczciwiec. Wspominamy o
ojcu, bo prawdopodobnie jemu zawdzięczamy porednio sukcesy syna. Bonaccio, pizański
kupiec, był szefem włoskiej kolonii w północno-afrykańskim porcie Boużia (dziś algierska
Beżaja). Tam Leonardo pobierał pierwsze lekcje matematyki u arabskiego nauczyciela.
Widocznie dobrze się sprawował bo dalsze studia zawiodły go w rozliczne miejsca. Były to
Egipt, Syria, Prowansja, Grecja i Sycylia - nieźle jak na 12-wiecznego studenta. Po powrocie
do Pizy, w 1202 roku, Leonardo napisał swoje głośne dzieło Liber Abaci
(Księga Rachunków), w której pojawiają się, i to w pierwszym rozdziale, arabskie a raczej
hinduskie cyfry. Warto tu wspomnieć, że ten dla nas tak dzisiaj naturalny system, wędrował do
Europy za pośrednictwem Arabów dobre parę setek lat.
To warto zobaczyć - jak hinduskie znaczki, za pośrednictwem przedsiębiorczych Arabów, docierały do Europy. Nota bene: słynny wynalazek hinduski - zero,
pojawiło się około IV-V wieku po Chrystusie, początkowo w formie kropki. Wraz z jego pojawieniem rozpoczął się dziesiętny system pozycyjny.