Na początek coś z fizyki rozrywkowej. Przypuśćmy, że chcemy ułożyć
na stole stos kart, tak aby
nawis utworzony przez karty
wystające poza krawędź stołu był maksymalny. Oczywiście
jeżeli ,,stos'' składa się z
jednej karty kładziemy ją
tak, aby środek masy karty przypadał na krawędzi stołu. (Wszystkie karty
kładziemy tak, aby ich
krótsze brzegi były
równoległe do krawędzi stołu). W przypadku dwóch kart karta
dolna ,,robi za stół'' , to
znaczy środek masy
karty górnej leży nad krawędzią dolnej, natomiast środek masy
całej struktury (dwóch kart)
- nad krawędzią stołu.
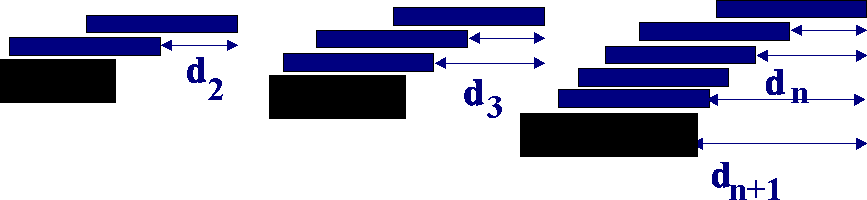
Rekurencja wygląda dość prosto. Najwygodniej będzie oznaczyć
przez dn odległość
krawędzi karty
,,wierzchniej'' od krawędzi karty n-tej od góry. Wówczas d1=0,
natomiast dla stosu n kart, dla
którego
stół ,,robi'' za kartę (n+1)-szą, dn+1 to współrzędna
środka masy układu n
kart. Znowu dla wygody
przyjmijmy długość karty równą dwóm jednostkom.
Współrzędna środka masy karty
o numerze k (cały czas
liczymy je od góry), liczona względem prawego brzegu nawisu to
odległość dk
powiększona o połowę
długości karty, a więc dk+1. Dla n kart mamy, zgodnie z definicja
środka masy:
Powyższy wzór warto przekształcić do postaci jawnej rekurencji.
Kładąc raz n=k, a raz n=k-1 mamy:
Odejmujemy równania stronami:
|
kdk+1 - (k-1) dk = 1 +dk
|
(1) |
a więc
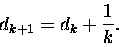 |
(2) |
Pierwsza karta wystaje o jedną jednostkę poza drugą, druga - o
pół jednostki poza trzecią,
trzecia - o jedną
trzecią jednostki poza czwartą, .... Jeżeli to nie wynika z rysunku to
przepraszam, robiłem go
całkowicie na
oko.
Pamiętając, że d1 = 1 i
stosując wzór k-krotnie
dostaniemy:
gdzie liczbę Hk nazywamy k-tą liczbą harmoniczną.
Przypominam: średnia harmoniczna
dwóch (lub
więcej) liczb to odwrotność sumy ich odwrotności. Na przykład
oporność zastępcza
układu oporników
połączonych równolegle jest równa średniej harmonicznej
poszczególnych oporności.
Wiemy wszyscy, że nieskończona suma
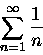 |
(3) |
jest rozbieżna. Ale jeżeli górna granica jest skończona (k) to mamy
liczbę harmoniczną,
która oczywiście
rośnie wraz ze wzrostem k, ale wzrost ten jest irytująco powolny. Na
początku (dla małych k)
jeszcze
idzie wytrzymać. Na przykład
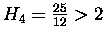 ,
a więc
wystarczy ułożyć na sobie
cztery karty, aby ta
wierzchnia znalazła się całkowicie poza krawędzią stołu. Potem
jednak liczby harmoniczne
rosną powolutku. Liczba o wskaźniku 1 000 000 (milion!),
H1000000 to skromne 14 z groszami.
Śliczny przykład podają autorzy matematyki konkretnej:
,
a więc
wystarczy ułożyć na sobie
cztery karty, aby ta
wierzchnia znalazła się całkowicie poza krawędzią stołu. Potem
jednak liczby harmoniczne
rosną powolutku. Liczba o wskaźniku 1 000 000 (milion!),
H1000000 to skromne 14 z groszami.
Śliczny przykład podają autorzy matematyki konkretnej:
Powolny, ale wytrwały robaczek R rozpoczyna wędrówkę od
początku metrowej gumowej
taśmy i pełznie
- z prędkością 1 centymetr na minutę - w kierunku jej końca.
Pod koniec każdej minuty
równie wytrwały
właściciel taśmy W, którego wyłącznym celem w życiu jest
pokrzyżowanie planów
R, rozciąga taśmę
równomiernie o 1 metr. Po jednej minucie R jest odległy o 1 cm od
początku swojej drogi i o 99 cm od
jej końca.
Wówczas W rozciąga taśmę o jeden metr, ale tak, że R zachowuje
swoja względną
pozycję, czyli 1% od startu i
99% od finiszu. Zatem R znajduje się 2 cm od punktu wyjścia i 198 od
celu. Po następnej minucie R
osiąga 3
cm taśmy, ma przed sobą 197 cm do przejścia i w tym momencie W
rozciąga taśmę.
Odpowiednie odległości
przyjmują wartości 4,5 i 295,5 cm. I tak dalej....
Na pierwszy rzut oka nie wydaje się w ogóle możliwe aby dzielny
robaczek kiedykolwiek dotarł do
mety. Ale
matematyka jest nieubłagana. Powyższy dość skomplikowany
schemat można streścić
prosto: w ciągu pierwszej
minuty R przebywa jedną setną swojej drogi, w ciągu drugiej -
jedną dwusetną, w ciągu
trzeciej - jedną
trzechsetną. Po n minutach R pokonuje
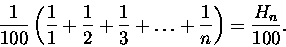
Wystarczy więc znaleźć wskaźnik n dla którego Hn
przekroczy sto. Mimo
żółwiego tempa przyrostu liczb
harmonicznych wiemy, że prędzej czy później to nastąpi, bo
nieskończona suma 3 jest
przecież rozbieżna.
Warto prześledzić ten sam przykład ale z ,,super-robaczkiem'', który
wędruje z prędkością pół metra na minutę. W pierwszej
minucie przebywa pół całkowitej drogi, w następnej - jedną
czwartą, w trzeciej - jedną szóstą. Po trzech minutach ma
przebyte:
1/2 + 1/4 + 1/6 = 11/12 drogi. Ponieważ w
czwartej minucie przebyłby
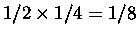 -mą drogi, to widać
że osiągnie metę przed
upływem tej czwartej minuty. Rzeczywiście : po trzykrotnym
wydłużeniu taśmy o jeden metr jej
długość wynosi na początku czwartej minuty cztery metry, z
których superrobaczek ma już za
sobą 3 i 2/3. Potrzebuje 40 sekund do przebycia pozostałych
33 1/3 centymetrów. Możesz sprawdzić - H4 >2.
Wracając do naszego powolnego robaczka: i on skazany jest na sukces ale
.... Aby spróbować
oszacować jak wielkie jest n aby
-mą drogi, to widać
że osiągnie metę przed
upływem tej czwartej minuty. Rzeczywiście : po trzykrotnym
wydłużeniu taśmy o jeden metr jej
długość wynosi na początku czwartej minuty cztery metry, z
których superrobaczek ma już za
sobą 3 i 2/3. Potrzebuje 40 sekund do przebycia pozostałych
33 1/3 centymetrów. Możesz sprawdzić - H4 >2.
Wracając do naszego powolnego robaczka: i on skazany jest na sukces ale
.... Aby spróbować
oszacować jak wielkie jest n aby
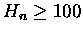 musimy skorzystać z
pewnych skojarzeń, dzięki
którym liczby harmoniczne staną się nam nieco bliższe.
musimy skorzystać z
pewnych skojarzeń, dzięki
którym liczby harmoniczne staną się nam nieco bliższe.
Każdy wie, że pochodna funkcji f(x),
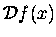 to
granica ilorazu różnicowego
to
granica ilorazu różnicowego
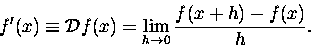 |
(4) |
W przypadku kiedy mamy do czynienia ze zmienną dyskretną, a nie
ciągłą, odpowiednikiem operatora 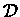 jest
operator różnicy
jest
operator różnicy 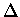 :
:
Byłoby sympatycznie, gdyby taki operator różnicowy posiadał własności
zbliżone do operatora
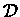 .
Podstawowa własność tego ostatniego to, na przykład,
.
Podstawowa własność tego ostatniego to, na przykład,
Niestety, analogiczny operator działający na dyskretne zmienne daje coś
zupełnie innego:
Aby operator różnicy zachowywał się wobec potęg dyskretnego
x-a podobnie jak jego starszy
kolega z dziedziny zmiennej ciągłej musimy ,,przedefiniować'' pojęcie
potęgi. Wprowadzamy
pojęcie ,,m-tej potęgi ubywającej''
Taka potęga pod działaniem operatora różnicy zachowuje się tak
jak trzeba:
Sprytne, prawda? O rachunku różnicowym można poczytać dużo
ciekawych rzeczy w literaturze (matematyce konkretnej). Dla naszych
celów wystarczy, jeżeli zdefiniujemy potęgę ubywającą z
ujemnym wykładnikiem.
Aby to zrobić popatrzmy na sekwencję potęg:
No tak. Obniżanie stopnia potęgi ubywającej dokonuje się - idąc
od góry - dzięki
sukcesywnemu dzieleniu: przez x-2, x-1 i x. jeżeli chcemy
kontynuować marsz w dół to
wydaje się logicznym, aby dzielić
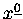 przez analogicznie
przyrastające liczby: x+1,
x+2, itd. I rzeczywiście:
przez analogicznie
przyrastające liczby: x+1,
x+2, itd. I rzeczywiście:
albo ogólnie:
Miało być o liczbach harmonicznych. I będzie! Tak jak w
rachunku różniczkowym mamy całki oznaczone, tak w rachunku
różnicowym
istnieją sumy oznaczone, a związki są analogiczne. Konkretnie, suma ubywających potęg x-
a, który to x zmienia się, ze skokiem jednostkowym, od a do b to
będzie odpowiednikiem naszej poczciwej całki
Powyższe wzory są OK dla 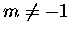 .
No właśnie. Całka
.
No właśnie. Całka
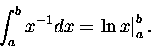 |
(5) |
A w rachunku różnicowym? szukamy funkcji f(x) takiej, że
Komputer zauważy, że taką funkcją jest właśnie liczba
harmoniczna, Hx:
Odkryliśmy karty - tajemnicze (?) liczby harmoniczne to odpowiedniki w
dziedzinie zmiennej dyskretnej
naszych starych, dobrych znajomych logarytmów naturalnych. Pamiętasz -
logarytm też należy do
rodzinki powolnych funkcji, iloraz
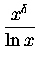 dąży do zera
przy
dąży do zera
przy
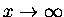 dla
każdego
dla
każdego 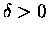 ! Mówiąc mało precyzyjnie a bardziej
obrazowo: dla dużych wartości
x zaciera się granica między zmienną ciągłą a dyskretną
(jednostkowy krok dyskretny staje
się malućki) i wtedy
! Mówiąc mało precyzyjnie a bardziej
obrazowo: dla dużych wartości
x zaciera się granica między zmienną ciągłą a dyskretną
(jednostkowy krok dyskretny staje
się malućki) i wtedy 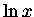 i Hx to praktycznie jeden diabełek.
i Hx to praktycznie jeden diabełek.
Prawdę mówiąc nie musieliśmy aż tak uczenie kombinować. To,
że liczba harmoniczna jest bliską kuzynką logarytmu naturalnego można
łatwo zobaczyć z dwóch podanych niżej rysuneczków. Czerwona
krzywa to wykres
f(x) = 1/x, a klocki stojące na osi poziomej to kolejne
wartości 1/n. Logarytm 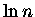 można wyrazić przy pomocy całki
można wyrazić przy pomocy całki
Całka ta - pole pod krzywą 1/x - musi być ,,z grubsza'' równa polu
poskładanemu z n kolejnych klocków - Sn. Jeżeli klocki
stawiać z prawej strony
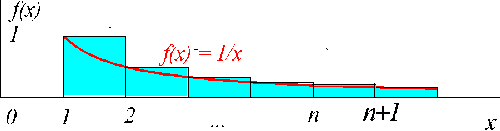
kolejnych wartości n to widzimy, że pole pod krzywą jest
mniejsze od Sn, która to suma to nic innego jak Hn:
Natomiast stawiając n klocków z lewej strony
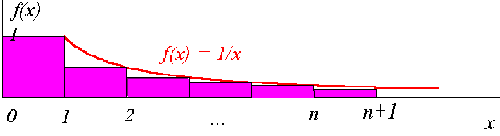
widzimy, że pole
powierzchni n klocków jest mniejsze od sumy: pole powierzchni pierwszego
prostokąta (=1) plus pole powierzchni pod krzywą f(x) (cały czas w granicach
od 1 do n):
Tak więc n-ta liczba harmoniczna jest dość dobrze zlokalizowana:
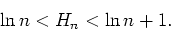 |
(6) |
Możemy zacieśnić pułapkę, w której tkwi Hn.
Uogólniona liczba harmoniczna Hn(p) zdefiniowana jest jako
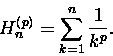 |
(7) |
Sumujemy odwrotności p-tych potęg liczb 1,2,....
p nie musi być całkowite, ale zwykle jest; już dla p>1) powyższa suma ma granicę przy
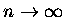 :
:
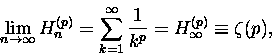 |
(8) |
która nazywa się ,,zetą Riemanna'' .Dla p=2, na przykład,
(Istnieje pół tuzina standardowych sposobów wykazania tej równości
- rachunek reziduów, liczby Bernoulliego, iloczyny nieskończone, itp.)
O liczeniu zety Riemanna dla parzystych argumentów jest mowa na stronie o liczbach Bernoulliego.
Jeżeli już wprowadzimy uogólnione liczby harmoniczne to związek
między ,,zwykłymi'' liczbami harmonicznymi a logarytmem da się
przedstawić bardzo zgrabnie. Korzystamy z Taylorowskiego rozwinięcia
logarytmu
podstawiając nieco inny argument logarytmu:
Ten szereg jest zbieżny dla k>1 (
|x| = 1/k < 1), a jego lewa strona to
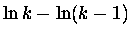 .
Sumując obie strony po k od 2 do n mamy
.
Sumując obie strony po k od 2 do n mamy
Ocierając pot z czoła
a w granicy, przy
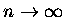
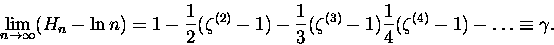 |
(9) |
Stała 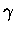 to stała Eulera-Mascheroniego. Euler obliczył ją w
swoim De progressionibus harmonicis observationes, artykule wydanym w
Petersburskich Commentarii academiae scientiarum imperialis Petropolitanae
w roku 1734, jako (w przybliżeniu) równą 0,577218. Dzisiaj artyści od
asymptotyki liczą rozwinięcia gammy zawierające tysiące cyfr po
przecinku i ...gryzą paznokcie z nerwów, bo nikomu nie udało się
jeszcze rozstrzygnąć problemu czy ta ,,połówka i ciut'' jest liczbą
wymierną czy nie. W każdym razie ograniczenie 6 Hn jest już
nieźle uściślone - Hn siedzi w około 58% drogi pomiędzy
to stała Eulera-Mascheroniego. Euler obliczył ją w
swoim De progressionibus harmonicis observationes, artykule wydanym w
Petersburskich Commentarii academiae scientiarum imperialis Petropolitanae
w roku 1734, jako (w przybliżeniu) równą 0,577218. Dzisiaj artyści od
asymptotyki liczą rozwinięcia gammy zawierające tysiące cyfr po
przecinku i ...gryzą paznokcie z nerwów, bo nikomu nie udało się
jeszcze rozstrzygnąć problemu czy ta ,,połówka i ciut'' jest liczbą
wymierną czy nie. W każdym razie ograniczenie 6 Hn jest już
nieźle uściślone - Hn siedzi w około 58% drogi pomiędzy 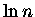 a
a 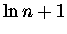 .
Jeżeli Cię to jeszcze nie zadowala, to konkretni matematycy podają lepszy
wzór
.
Jeżeli Cię to jeszcze nie zadowala, to konkretni matematycy podają lepszy
wzór
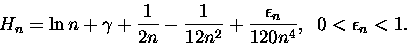 |
(10) |
Wracamy do dzielnego robaczka i jego wędrówki, realizowanej na przekór niecnym knowaniom
obrzydliwego właściciela gumowej taśmy. Robaczek dopadnie mety gdy
Hn przekroczy 100. Z podanych wyżej oszacowań wynika, że będzie
to dla n równego z grubsza
Nastąpi to - bagatela - w około 287 decylionów wieków od
rozpoczęcia wędrówki. Gumowa taśma rozciągnie się do
długości ponad 1027 lat świetlnych, a jej cząsteczki będą
bardzo, bardzo daleko od siebie...

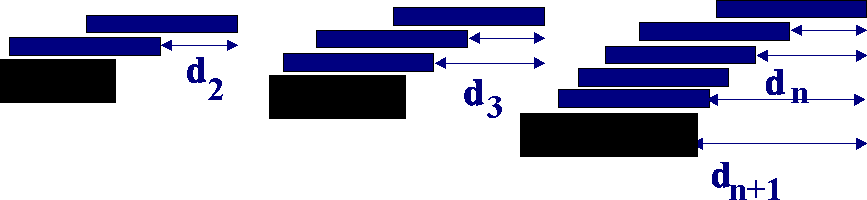
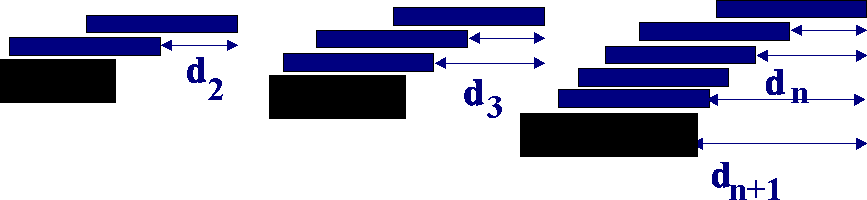
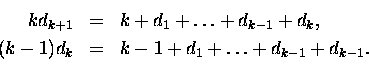
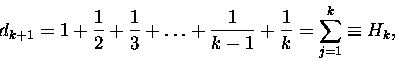
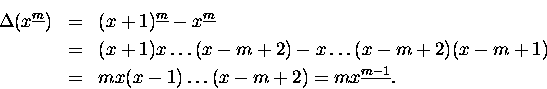
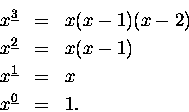
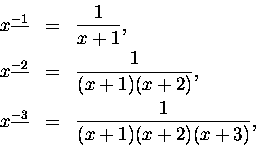
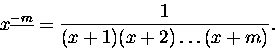
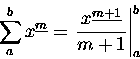
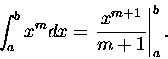
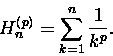
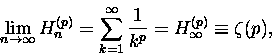
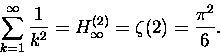
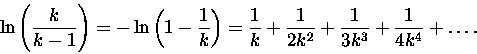
![\begin{eqnarray*}\lefteqn{ \sum_{k=2}^n [\ln k - \ln(k-1)] = \ln n - \ln 1 = \ln...
...) + \frac 1 3 (H_n^{(3)}-1)
+ \frac 1 4 (H_n^{(4)}-1) + \ldots. \end{eqnarray*}](hmg45.gif)
