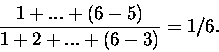
 Z tych trzech nazwisk "uchowało" się głównie jedno - wszyscy wiemy na czym polega zawieszenia Cardana, a także pamiętamy (?) wzory Cardana
na znajdowanie pierwiastków równania trzeciego stopnia. (N.B. ten ostatni problem, spowodował "przypadkowe odkrycie" liczb zespolonych).
Z tych trzech nazwisk "uchowało" się głównie jedno - wszyscy wiemy na czym polega zawieszenia Cardana, a także pamiętamy (?) wzory Cardana
na znajdowanie pierwiastków równania trzeciego stopnia. (N.B. ten ostatni problem, spowodował "przypadkowe odkrycie" liczb zespolonych).
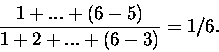
Z kolei Tartaglia uważał, że podział powinien być dokonany w stosunku
gdzie z to liczba zwycięstw potrzebnych do wygrania,
a ![]() - to liczby zwycięstw obu ekip. W tej konkretnej sytuacji należałoby dzielić
w stosunku 4:2. Ale - mimo, że wszyscy trzej byli z pewnością świetnymi
matematykami, to żaden z nich nie podał poprawnej odpowiedzi! Na tę ostatnią
trzeba na nią było czekać 150 lat, a zawdzięczamy ją Pascalowi. To on podał
właśnie poprawny schemat rozumowania : należy rozważyć wszystkie
możliwe sekwencje w maksymalnej liczbie gier, jakie mogą być jeszcze rozegrane.
Takich gier może być co najwyżej trzy, a sekwencje to
- to liczby zwycięstw obu ekip. W tej konkretnej sytuacji należałoby dzielić
w stosunku 4:2. Ale - mimo, że wszyscy trzej byli z pewnością świetnymi
matematykami, to żaden z nich nie podał poprawnej odpowiedzi! Na tę ostatnią
trzeba na nią było czekać 150 lat, a zawdzięczamy ją Pascalowi. To on podał
właśnie poprawny schemat rozumowania : należy rozważyć wszystkie
możliwe sekwencje w maksymalnej liczbie gier, jakie mogą być jeszcze rozegrane.
Takich gier może być co najwyżej trzy, a sekwencje to
gdzie A oznacza zwycięstwo pierwszej, a B
- drugiej ekipy. Jak widać siedem (na osiem możliwych) sekwencji zapewnia
zwycięstwo pierwszej ekipie, a więc premia powinna być podzielona w stosunku
1 :7. Oczywiście, taki wynik można też uzyskać na gruncie modelu rozkładu
dwumianowego (Bernoulliego). W obu przypadkach zakładamy, że w pojedynczej
grze obie ekipy mają jednakowe szanse na wygranie. Problem można
nieco skomplikować, jeżeli szanse obu ekip określać na podstawie dotychczasowych
wyników.
