


Next: indukcja matematyczna
Up: Kilka drobiazgów z historii
Previous: Gracze zaczynają liczyć swoje
 Blaise Pascal (1623-1662), to matematyk i fizyk, który ostatnie osiem lat swojego krótkiego niestety
życia
poświęcił bez reszty działalności religijnej i filozoficznej (był rzecznikiem jansenistów).
Pascal od dziecka był
geniuszem
matematycznym, uczestnikiem elitarnego kółka (dorosłych) matematyków, skupionych wokół
ojca Mersenne
(poszukiwania tzw. doskonałych liczb) Ojciec Błażeja, Etienne Pascal, sędzia, w roku 1639
został zarządcą
urzędu
podatkowego dla Normandii. Blaise jako dobry syn spędził kilka lat
nad konstrukcją maszyny do liczenia
,
Blaise Pascal (1623-1662), to matematyk i fizyk, który ostatnie osiem lat swojego krótkiego niestety
życia
poświęcił bez reszty działalności religijnej i filozoficznej (był rzecznikiem jansenistów).
Pascal od dziecka był
geniuszem
matematycznym, uczestnikiem elitarnego kółka (dorosłych) matematyków, skupionych wokół
ojca Mersenne
(poszukiwania tzw. doskonałych liczb) Ojciec Błażeja, Etienne Pascal, sędzia, w roku 1639
został zarządcą
urzędu
podatkowego dla Normandii. Blaise jako dobry syn spędził kilka lat
nad konstrukcją maszyny do liczenia
, ,
który
miałby pomóc ojcu w uciążliwych rachunkach. W ciągu 10 lat
opracował podobno 50 modeli takiego mechanicznego kalkulatora, który zresztą świetnie
działał. Pascal miał
nadzieję, że opatentowana
wersja uczyni go bogatym. Niestety - znakomita maszyna okazała się
...za droga.
Zainteresowanie Pascala statystyką rozbudził Antoine
Gombaud (16071684), Chevalier de Méré, żołnierz,
podróżnik (zawędrował nawet do Ameryki, co na owe
czasy było nie lada przedsięwzięciem), arbiter elegantiarum (pisał podręczniki dobrych
manier !) i ...
gracz w kości. Miał o sobie niezłe mniemanie jako matematyku. Jego problem był
następujący: otóż, de Mere
potrafił obliczyć, że potrzebuje czterech rzutów jedną kostką do skutecznego (tzn. z szansami
nieco większymi
od 50 %)
obstawienia zakładu, że uda mu się wyrzucić szóstkę.
Rzeczywiście takie prawdopodobieństwo, wynosi ,,pewność -
4
,
który
miałby pomóc ojcu w uciążliwych rachunkach. W ciągu 10 lat
opracował podobno 50 modeli takiego mechanicznego kalkulatora, który zresztą świetnie
działał. Pascal miał
nadzieję, że opatentowana
wersja uczyni go bogatym. Niestety - znakomita maszyna okazała się
...za droga.
Zainteresowanie Pascala statystyką rozbudził Antoine
Gombaud (16071684), Chevalier de Méré, żołnierz,
podróżnik (zawędrował nawet do Ameryki, co na owe
czasy było nie lada przedsięwzięciem), arbiter elegantiarum (pisał podręczniki dobrych
manier !) i ...
gracz w kości. Miał o sobie niezłe mniemanie jako matematyku. Jego problem był
następujący: otóż, de Mere
potrafił obliczyć, że potrzebuje czterech rzutów jedną kostką do skutecznego (tzn. z szansami
nieco większymi
od 50 %)
obstawienia zakładu, że uda mu się wyrzucić szóstkę.
Rzeczywiście takie prawdopodobieństwo, wynosi ,,pewność -
4 nie-szóstka'', czyli
nie-szóstka'', czyli
1 - (5/6)4 = 1 - 625/1296 > 0.5.
Ten wynik de Mere próbował uogólnić na przypadek gry dwoma kostkami. Już Cardano
określił ,,przestrzeń
zdarzeń'' dla dwóch kostek:
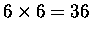 możliwości. De Mere próbował przenieść mechanicznie
proporcję z rzutów jedną kostką -
możliwości. De Mere próbował przenieść mechanicznie
proporcję z rzutów jedną kostką -
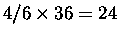 ,
a więc
zakładał się, że wyrzuci dwie szóstki w przynajmniej 24 rzutach i
...przegrywał! Rzeczywiście, żeby grać bezpiecznie
potrzebnych rzutów jest 25:
,
a więc
zakładał się, że wyrzuci dwie szóstki w przynajmniej 24 rzutach i
...przegrywał! Rzeczywiście, żeby grać bezpiecznie
potrzebnych rzutów jest 25:
De Mere był tak wzburzony niepowodzeniem1.2, że napisał o tym do Pascala.
Ten - dał się wciągnąć się i w dodatku wciągnął do konsultacji samego Pierre'a Fermat
(tak, tak, tego od zasady
Fermata w fizyce i wielkiego i małego twierdzenia Fermata w teorii liczb). Owocem tych zainteresowań (i
jak
tu nie mówić, że i niewłaściwe zainteresowania mogą
spowodować pozytywne skutki!) był opublikowany 1654 Traité du
triangle arithmétique, kopalnia użytecznych relacji pomiędzy współ
czynnikami dwumianowymi1.3, znanymi właśnie pod
nazwą ,,trójkąta Pascala''. Te współczynniki występują
też we wzorze (niezbyt chyba słusznie nazywanym wzorze Newtona,
skoro znali go już, wprawdzie dla niewielkich n, ...sumeryjscy rachmistrzowie, 2 tysiące lat przed
Chrystusem):
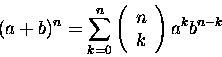 |
(1.1) |
jako symbole
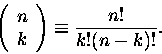 |
(1.2) |
Trójkąt Pascala1.4, utworzony z kolejnych wartości
współczynników 1.2
może być użyty do
rozwiązania problemów typu gry w balla: np. gramy do czterech
zwycięstw, przeciwnik ma już jedną wygraną - jakie mam szanse?
Konstruujemy trójkąt Pascala dla n=6 (jest to maksymalna liczba gier
jakie mogą się odbyć), czyli wyliczamy po kolei współczynniki
1.2, dla
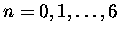 :
:
(Wiesz zapewne, że każdy wyraz (poza skrajnymi jedynkami) kolejnego
wiersza obliczamy dodając do siebie jego sąsiadów z lewej i
prawej strony w poprzednim wierszu.)
Wystarczy więc przyglądnąć się ostatniemu, siódmemu wierszowi.
Mamy
2n = 26 = 64 możliwości różnych sekwencji zwycięstw.
Jest 1 (tylko) szansa na moich 6 kolejnych zwycięstw, 6 - na
pięć (przeciwnik wygrywa tylko raz), 15 - na cztery (przy
dwóch przeciwnika). Wszystkie pozostałe scenariusze prowadzą do
mojej przegranej. Moje szanse wygrania całej partii to
1 + 6 + 15 = 22
do 64, a więc trochę więcej niż jedna trzecia.
O ile Pascal nie był ,,prawdziwym ojcem'' swojego trójkąta,
to z dużą dozą pewności można go uznać za ,,ojca'' metody indukcji matematycznej.




Next: indukcja matematyczna
Up: Kilka drobiazgów z historii
Previous: Gracze zaczynają liczyć swoje
Andrzej Lenda
1999-03-08
 Blaise Pascal (1623-1662), to matematyk i fizyk, który ostatnie osiem lat swojego krótkiego niestety
życia
poświęcił bez reszty działalności religijnej i filozoficznej (był rzecznikiem jansenistów).
Pascal od dziecka był
geniuszem
matematycznym, uczestnikiem elitarnego kółka (dorosłych) matematyków, skupionych wokół
ojca Mersenne
(poszukiwania tzw. doskonałych liczb) Ojciec Błażeja, Etienne Pascal, sędzia, w roku 1639
został zarządcą
urzędu
podatkowego dla Normandii. Blaise jako dobry syn spędził kilka lat
nad konstrukcją maszyny do liczenia
,
Blaise Pascal (1623-1662), to matematyk i fizyk, który ostatnie osiem lat swojego krótkiego niestety
życia
poświęcił bez reszty działalności religijnej i filozoficznej (był rzecznikiem jansenistów).
Pascal od dziecka był
geniuszem
matematycznym, uczestnikiem elitarnego kółka (dorosłych) matematyków, skupionych wokół
ojca Mersenne
(poszukiwania tzw. doskonałych liczb) Ojciec Błażeja, Etienne Pascal, sędzia, w roku 1639
został zarządcą
urzędu
podatkowego dla Normandii. Blaise jako dobry syn spędził kilka lat
nad konstrukcją maszyny do liczenia
, ,
który
miałby pomóc ojcu w uciążliwych rachunkach. W ciągu 10 lat
opracował podobno 50 modeli takiego mechanicznego kalkulatora, który zresztą świetnie
działał. Pascal miał
nadzieję, że opatentowana
wersja uczyni go bogatym. Niestety - znakomita maszyna okazała się
...za droga.
Zainteresowanie Pascala statystyką rozbudził Antoine
Gombaud (16071684), Chevalier de Méré, żołnierz,
podróżnik (zawędrował nawet do Ameryki, co na owe
czasy było nie lada przedsięwzięciem), arbiter elegantiarum (pisał podręczniki dobrych
manier !) i ...
gracz w kości. Miał o sobie niezłe mniemanie jako matematyku. Jego problem był
następujący: otóż, de Mere
potrafił obliczyć, że potrzebuje czterech rzutów jedną kostką do skutecznego (tzn. z szansami
nieco większymi
od 50 %)
obstawienia zakładu, że uda mu się wyrzucić szóstkę.
Rzeczywiście takie prawdopodobieństwo, wynosi ,,pewność -
4
,
który
miałby pomóc ojcu w uciążliwych rachunkach. W ciągu 10 lat
opracował podobno 50 modeli takiego mechanicznego kalkulatora, który zresztą świetnie
działał. Pascal miał
nadzieję, że opatentowana
wersja uczyni go bogatym. Niestety - znakomita maszyna okazała się
...za droga.
Zainteresowanie Pascala statystyką rozbudził Antoine
Gombaud (16071684), Chevalier de Méré, żołnierz,
podróżnik (zawędrował nawet do Ameryki, co na owe
czasy było nie lada przedsięwzięciem), arbiter elegantiarum (pisał podręczniki dobrych
manier !) i ...
gracz w kości. Miał o sobie niezłe mniemanie jako matematyku. Jego problem był
następujący: otóż, de Mere
potrafił obliczyć, że potrzebuje czterech rzutów jedną kostką do skutecznego (tzn. z szansami
nieco większymi
od 50 %)
obstawienia zakładu, że uda mu się wyrzucić szóstkę.
Rzeczywiście takie prawdopodobieństwo, wynosi ,,pewność -
4
