


Next: Rodzina Bernoullich
Up: Blaise Pascal
Previous: Blaise Pascal
Sposób dowodzenia twierdzeń matematycznych, odnoszących się do liczb całkowitych.
Takie twierdzenie
sprowadza się zazwyczaj do pewnej propozycji P(n), która - jak przypuszczamy odnosi się
do zbioru
wszystkich liczb całkowitych, lub przynajmniej do pewnego ich podzbioru (np. dla wszystkich
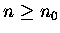 ,
gdzie n0 jest pewną ustaloną wartością.
Podkreślmy słowo przypuszczamy - metoda indukcja nie odkryje nam pewnej
własności, ale
pozwoli udowodnić taką własność, którą - w oparciu np. o pewne przesłanki
,,empiryczne'' - podejrzewamy o
istnienie.
Metoda indukcji składa się z dwóch etapów:
,
gdzie n0 jest pewną ustaloną wartością.
Podkreślmy słowo przypuszczamy - metoda indukcja nie odkryje nam pewnej
własności, ale
pozwoli udowodnić taką własność, którą - w oparciu np. o pewne przesłanki
,,empiryczne'' - podejrzewamy o
istnienie.
Metoda indukcji składa się z dwóch etapów:
- 1.
- Wykazujemy słuszność P(n) dla pewnego ustalonego n=n0. Zwykle n0 = 1, bo zwykle
dowody
indukcyjne odnoszą się do całego zbioru dodatnich liczb całkowitych. Dla n0=1 ewentualne
rachunki są też
najprostsze!
- 2.
- Zakładamy, że P(n) jest prawdziwe i w oparciu o to założenie udowadniamy
prawdziwość naszego
przypuszczenia dla n= n+1, a więc wykazujemy słuszność P(n+1).
Typowym przykładem metody indukcji może być na przykład wykazanie wzoru na sumę sześcianów
pierwszych n
dodatnich liczb całkowitych:
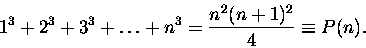 |
(1.3) |
Zgodnie ze schematem zaczynamy od ,,sprawdzenia'' hipotezy dla n=1. Mamy
Następnie zakładamy słuszność P(n) dla n=k
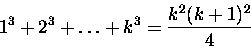 |
(1.4) |
i próbujemy
udowodnić ją dla n=k+1. dodajemy do obu stron 1.4 (k+1)3:




Next: Rodzina Bernoullich
Up: Blaise Pascal
Previous: Blaise Pascal
Andrzej Lenda
1999-03-08
![\begin{eqnarray*}1^3 + 2^3 +\ldots + k^3 + (k+1)^3 &=& \frac{k^2(k+1)^2}{4} + (k...
...
& = & \frac{(k+1)^2[(k + 2)^2]}{4}; \hfill \mbox{\em c.b.d.o.}
\end{eqnarray*}](img19.gif)
